MATEMÀTIQUES BÀSIQUES
(última actualització: 4/3/2011 . Pendent de correcció ortogràfica)
Regles d’ordre d’operacions
A diari fem moltes activitats que requerèixen un ordre concret (primer aixeques la tapa de vàter i desprès seus a fer les teves coses, no al revès). Igualment, quan realitzem operacions matemàtiques diferents haurem de seguir un ordre concret per resoldre correctament el problema. L’ordre és:
1. Resoldre parèntesi, claudators o claus “de dins cap a fora” ( ) [ ] { }
2. Resoldre exponents o arrels.
3. Multiplicacions i divisions d’esquerra a dreta.
4. Sumes i restes d’esquerra a dreta.
Si ens trobem amb una combinació de sumes i multiplicacions, sempre multiplicarem primer.
Exemple:
3+4*5= 3+20= 23
I no farem mai: 3+4*5= 7*5= 35
perquè es donès aquest cas hauríem de tenir el problema expressat amb parèntesi així: (3+4)*5
Davant de sumes i restes consecutives podem sumar d’una banda tots els possitius i per l’altra tots els negatius i finalment sumem els dos nombres
Exemple
+3-4+5-6+45-8=(+3+5+45)+(-4-6-8)= +53+(-18)= 53-18=35
Mínim comú múltiple
El mínim comú múltiple (m.c.m.) de dos o més nombres naturals és el menor nombre natural que és múltiple de tots ells. Per determinar el m.c.m. Descomposem cada nombre en factors primers i l’expressem com a producte dels seus factor primers. El m.c.m. serà el resultat de multiplicar els factors comuns y no comuns elevats a la potència més gran.
Exemple:
Trobar el m.c.m. de 72 i 56.
Primer descomposem els nombres en factors primers
72 2 56 2
36 2 28 2
18 2 14 2
9 3 7 7
3 3 1
1
Expressem els nombre com a producte dels seus factor primers.
72= 2 3 x32 56= 23 x7
Finalment el m.c.m. serà el resultat de multiplicar els factors comuns y no comuns elevats a la potència més gran. M.c.m (72,56)= 2 3 x32 x7= 8x9x7 = 504 Guay, no?
Operacions amb fraccions
-Reducció de fraccions
Hem de reduïr (o simplificar) els resultats en forma de fracció dels nostres problemes quan això sigui possible. Per reduïr una fracció es divideix el numerador i el denominador per un mateix número, resultant una fracció equivalet, però expressada amb nombres més petits
Per reduïr “3/6” dividim tant el numerador com el denominador per “3”, resultant 1/3
-Suma i resta de fraccions
amb el mateix denominador
: es sumen o es resten els numeradors i es manté el denominador.
1/4+2/4= 3/4 1/4-3/4= -1/4
-Suma i resta de fraccions amb diferent denominador
2/3+1/4=
1. Determinem el denominador comú, el qual serà el mínim comú múltiple dels denominadors.
m.c.m. (3,4)= 12
2. Aquest denominador comú es divideix per cadascún dels denominadors i es multiplica el cocient obtingut pel numerador corresponent.
(12:3)x2/12 + (12/4)x1/12=
3. Es sumen o resten els numeradors de les fraccions equivalents obtingudes.
6/12+3/12=9/12 Reduïnt= 3/4
-Multiplicació de fraccions
Multipliquem entre sí els numeradors i el resultat serà el nou numerador
Multipliquem entre sí els denominadors i el resultat serà el nou denominador
5/2X8/3=5X8/2X3=40/6 Reduïnt= 20/3
-Divisió de fraccions
Multipliquen “en creu”: El numerador de la primera fració multiplicat pel denominador de la següent ens donarà el numerador del resultat. El denominador de la primera fració multiplicat pel numerador de la següent ens donarà el denominador del resultat
2/3:5/4= 2x4/3x5= 8/15
Arrels quadrades
Les arrels es representen mitjançant el símbol √ que es denomina radical. És l’operació contrària al quadrat o potència de 2. Per exemple "√81" es llegeix: "arrel quadrada de 81". El resultat és "9" perquè 92=81. Arrels quadrades exactes són aquelles que tenen un resultat sense decimals. Les arrels quadrades exactes més comuns són:
√1=1 √4=2 √9=3 √16=4 √25=5 √36=6 √49=7 √64=8 √81=9 √100=10 √121=11 √144=12 √169=13 √196=14 √225=15 √256=16 √289=17 √324=18 √361=19 √400=20
Les arrels quadrades inexactes tenen un resultat en forma de nombre decimal. Per exemple el nombre 38 no és un quadrat perfecte. Està comprès entre els quadrats perfectes 36 (62) i 49 (72). El nombre resultant està comprès entre l’arrel quadrada
de 6 i de 7. Per tant: l’arrel quadrada de 38 és igual a 6 (la part entera) i la diferència (38-36) =5 (residu de l’arrel quadrada).
No aprendrem a resoldre arrels quadrades de nombres grans amb el sistema-ortodoxe-que-te-cagas perquè 1) Els aspirants a superar la E.S.O. podeu fer servir calculadora 2) Els que us trobeu amb un bitxo d’aquests en una oposició perdreu un temps preciòs fents nombroses operacions 3) l’explicació és llarga i farragosa i em trenca la estètica del resum. Trobem la solució per aproximació.
El mateix serveix per les arrels cúbiques, les exactes més freqüents de les quals son:
3√1=1 3√8=2 3√27=3 3√64=4 3√125=5 3√216=6 3√343=7 3√512=8 3√729 = 9 3√1000 = 10 3√1331 = 11 3√1728=12 3√2197=13 3√2744=14 3√3375=15
Equacions d’una incògnita
Una equació és una igualtat que conté una o diverses incògnites. Resoldre l’equació consisteix en determinar els valors que pot prendre la incògnita (generalment representades per les lletres "x", "y", etc.) per fer verdadera la igualtat. Per resoldre una equació amb una incògnita haurem d’aillar-la a un costat de la igualtat i resoldre el que tenim a l’altra banda de dita igualtat.
Hem de tenir en compte que quan passem un nombre d’una a banda a l’altra de la igualtat canvia en la seva funció. És a dir:
Si estava sumant passará restant
Si estava restant passará sumant
Si estava multiplicant passará dividint (mantenint el seu signe original, positiu o negatiu)
Si estava dividint passará multiplicant (mantenint el seu signe original, positiu o negatiu)
Una potència de dos passará com arrel quadrada
Una arrel quadrada passará com potència de dos
etc.
Exemples:
x+1=3; x=3-1= 2
3x=3; x=3/3= 1
x-4=7; x=7+4= 11
x/3= 5; x=5x3= 15
Regles de 3
La regla de 3 és una forma de resolució de problemes de proporcionalitat entre 4 valors, un dels quals és una incògnita. Les regles de 3 són molt útils per resoldre problemes domèstics i quotidians (per exemple percentatges). I diguem-ho clarament: tú no contractaries ningú que no sapigués fer una simple regla de 3.
Regla de 3 simple directa: “A” és a “B” de la mateixa manera (proporcional) que “C” és a “D” (la nostra incògnita)
La representació clàssica seria
A --------->B
C --------->D i es resol plantejant-la així D= (CxB)/A
Exemples
3 comercials tenen una despesa de 153 € en dietes, Quanta despesa tindran 19 comercials? (com que no són molt originals gastaran la mateixa quantitat per persona)
3 persones ------------> 153 €
19 persones ----------> x € x= (153x19)/3; x= 2907/3; x= 969 €
Un partit de futbol dura 90 minuts. Si un equip ha tingut la pilota un total de 63 minuts, quin percentatge de tot el temps n’ha tingut la possessió?
90 minuts ---------------> 100% del temps
63 minuts ---------------> x% del temps x= (100x63)/90= 6300/90= 70%
Regla de 3 simple inversa: “A” és a “B” de manera inversament proporcional que “C” és a “D” (la nostra incògnita)
A --------->B
C --------->D i es resol plantejant-la així D= (AxB)/C
Exemple
A la càpsula espaial hi ha aire perque sobrevisquin 5 persones durant 12 dies. Si ens desfem de dues persones, quans dies podem sobreviure la resta?
5 persones ------------> 12 dies
3 persones ------------> x dies x=(5x12)/3; x=60/3; x=20 dies
Regla de 3 composta: aquí la cosa es complica, però nosaltres... això, con un par. La regla de 3 composta en realitat és una combinació de diferents regles de 3 simples que poden ser directes, inverses, o una combinació. Per resoldre-les (ja ho has endevinat) , fem primer la primera i desprès, seh, la segona, i així fins la victòria final.
Exemple
A la càpsula inter-espaial hi ha 20.000 litres d’aire, quantitat exacta perque sobrevisquin 5 tripulants durant 12 dies respirant normal. Quanta gent hauria d’haver a la nau per sobreviure 22 dies amb 15.000 litres d’aire? (calculem que necessitem 5.000 l. D’aire pel foc de la barbacoa). Dit d’una altra manera, a quants hem de sacrificar (a banda del capellà de la nau)?
5 tripulants ------------> 12 dies -------------->20.000 l. d’aire
x tripulants ------------> 22 dies -------------->15.000 l. D’aire
Fixeu-vos en la primera regla de tres, la que relaciona persones amb dies, i deduireu que és una regla inversa, perque quanta més gent, menys dies poden sobreviure. En canvi la segona, la que relaciona persones amb aire n’és directa perquè més persones necessiten més aire.
Plantegem la primera, la indirecta: x=(5x12)/22
Plantegem la segona, la directa: x= (5x15.000)/20.000
I seguidament unim ambdues fraccions sense repetir cap terme x= (5x12x15.000)/(20.000x22);
x= 900.000/440.000; x= 2,045454545. És a dir, dues persones poden sobreviure. El capellà i dos més tindran donc, un accident, i tu i la Comandant Ripley tindreu més temps per jugar a metges i arribar a la base.
Sistemes d’equacions amb dues incògnites
Els sisteme d’equacions amb dues incògnites serveixen per resoldre problemes on ens falten dues dades. De vegades ens donaran l’enunciat del problema i haurem de plantejar el sistema d’equacions per poder resoldre’l. Un exemple típic d’enunciat seria:
“En Pau i la seva filla carla tenen entre tots dos 50 anys. D’aquí 15 anys en Pau tindrà el triple d’edat que la seva filla. Quants anys tenen en Pau i la Carla?”
Plantejament:
Direm que En Pau és la incògnita “x” i que la seva filla Carla és la incògnita “y”.
La primera frase “En Pau i la seva filla Carla tenen entre tots dos 50 anys” la podem expressar doncs d’aquesta manera: x+y=50.
La segona frase ens diu que “ d’aquí 15 anys en Pau tindrà el triple d’edat que la seva filla”. Si l’edat actual d’en Pau és x, l’edat d’en Pau d’aquí a 15 anys serà x+15. Si l’edat actual de la Carla és y, d’aquí 15 any serà y+15. Si x+15 (l’edat d’en Pau d’aqui 15 anys) és el triple de y+15 (l’edat de la Isabel) llavors podem dir que x+15=3(y*15). La segona eqüació serà doncs: x+15=3(y+15)
el nostre sistema d’eqüacions quedaria plantejat de la següent manera:
x+y=50
x+15=3(y+15)
Mètodes per a la resolució algebraica de sistemes d’equacions
Tenim diferents mètodes per resoldre equacions i tot i que semblen d’entrada difícils d’entendre, en realitat només necessites posar una mica de carinyo perque et donim molta satisfacció. I per sempre, no et demanaran el divorci, treient-te una pensió compensatòria.
Igualació: consisteix en aïllar la mateixa incògnita a les dues equacions i igualar les noves equacions obtingudes:
1. Seleccionem una de las dues incògnites, per exemple la “x” i l’aïllem a les dues equacions.
Aïllant la “x” de la primera eqüació “x+y=50” ens resulta: x=50-y
Aïllant la “x” de la segona eqüació “x+15=3(y+15)” ens resulta: x=3(y+15)-15; x=3y+45-15; x=3y+30
2. Igualem les expressions resultants
50-y=3y+30
3. Resolem l’equació obtinguda obtenint el resultat de “y”
50-y=3y+30; 50-30=3y+y; 20=4y; y=20/4; y=5 (Edat de la Carla)
4. Sustituim “y” pels seu valor (5) en qualsevol de les equacions originals i resolem per obtenir el valor de “x”
x+y=50; x+5=50; x=50-5; x=45 (Edat d’en Pau)
5. Si volem comprovar si els resultats són els correctes només haurem de sustituir en qualsevol de les equacions originals les incògnites pels valor que hem obtingut i comprovar que la igualtat es cumpleix:
x+y=50; 45+5=50; 50=50
Substitució: consisteix en aïllar una de les incògnites en una de les equacions i substituir la seva expressió en la segona:
1. Aïllem una incognita, per exemple la “x”, d’una de les eqüacións
Aïllant la “x” de la primera eqüació “x+y=50” ens resulta: x=50-y
2. Substituim a l’altra equació la incognita aïllada (x) pel valor que hem obtingut (50-y)
(50-y)+15=3(y+15)
3. Resolem l’equació obtinguda, aconseguint el resultat de la incògnita “y”.
(50-y)+15=3(y+15); 50-y+15=3y+45; 50+15-45=3y+y; 20=4y; y=20/4; y=5 (Edat de la Carla)
4. Sustituim “y” pels seu valor (5) en qualsevol de les equacions originals i resolem per obtenir el valor de “x”
x+y=50; x+5=50; x=50-5; x=45 (Edat d’en Pau)
5. Si volem comprovar si els resultats són els correctes només haurem de sustituir en qualsevol de les equacions originals les incognites pels valor que hem obtingut i comprovar que la igualtat es cumpleix:
x+y=50; 45+5=50; 50=50
Reducció: consisteix en multiplicar una o amdues equacions per un nombre convenient i sumar o restar ambdues equacions per a obtenir una única equació amb una única incògnita:
1. Seleccionem una de les dues incògnites i igualem els coeficients en ambdues equacions. En el nostre cas les dues “x” son iguals i no hem de fer aquest pas
x+y=50
x+15=3(y+15)
2. Sumem o restem les equacions per obtenir una sola equació amb una sola incògnita.
En el nostre cas restem per eliminar la “x”, obtenint:
y-15=50-3y-45
3. Resolem l’equació obtinguda per aconseguir el resultat de la incògnita “y”.
y+3y=50-45+15; 4y=20; y=20/4; y=5 (Edat de la Carla)
4. Sustituim “y” pels seu valor (5) en qualsevol de les equacions originals i resolem per obtenir el valor de “x”
x+y=50; x+5=50; x=50-5; x=45 (Edat d’en Pau)
5. Si volem comprovar si els resultats són els correctes només haurem de sustituir en qualsevol de les equacions originals les incognites pels valor que hem obtingut i comprovar que la igualtat es cumpleix:
x+y=50; 45+5=50; 50=50
Cada métode és igualment vàlid per resoldre el sistema d’eqüacions. Podem fer servir qualsevol d’ells, tret que s’ens demani un en particular (sí, poden fer-ho, ells són així)
La comprovació no és necessària i no forma part de la mecànica per a obtenir el resultat, però és aconsellable fer-la perquè serà com detectarem possibles errors de càlcul.
Un cop trobada la incognita seleccionada trobar-ne l’altra és igual en els tres mètodes. Aquí he reproduït tots els passos en cada mètode perquè es vegi el desenvolupament complet o per si feu una consulta d’un mètode en particular
A cada exemple he aïllat o eliminat primer la “x” i hem obtingut primer la “y”. El resultat evidentment seria el mateix i igualment vàlid si haguéssim treballat primer amb la y. Les preferències personals o detectar en una primera ullada la facilitat de aillar una incògnita en particular són raons per començar per una o una altra.
b=base, a=alçada, π=pi=3,141592..., r=radi, B=base gran, D=diagonal gran, d=diagonal petita, h=hipotenusa, c=catet
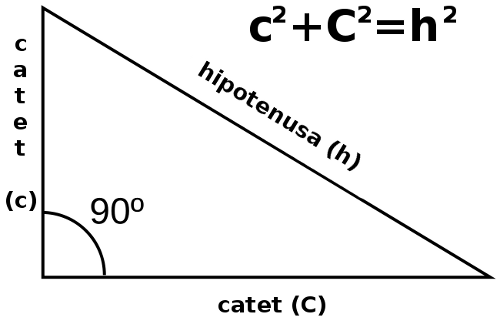
Teorema de Pitàgoras
h2=c2+c2
Perímetres
Cercle= 2π.r
Càlcul de superfícies (àrees)
b=base, a=alçada, π=pi=3,141592..., r=radi, B=base gran, D=diagonal gran, d=diagonal petita
Quadrat: b2 Rectangle: bxa Paralel.logram: bxa Triangle (bxa)/2 Trapeci= [(B+b)a]/2 Romb= (D.d)/2
Cercle= π.r2 Esfera= 4π.r2
Davant d’un polígon compost, mantenim la calma, respirem profundament i, en paraules de Jack the Ripper, “anem per parts”. Perque l’àrea d’un polígon compost s’obté sumant les àrees dels diferents polígons que composen la figura original. Chupao, no?
Càlcul de volums
Cub= superfície de la base x alçada
Esfera= (4π.r3)3
Davant del problema de calcular el volum d’una figura tridimensional complexa, enrecordeu-vos de nou de Jack the Ripper: “anem per parts”. Perquè el volum d’una figura composta s’obté sumant els volums dels diferents poliedres que composen la figura original. Fascinant, sí.
Notació científica (potències de deu)
font: viquipèdia: http://ca.wikipedia.org/wiki/Notaci%C3%B3_cient%C3%ADfica
101 = 10
102 = 100
103 = 1000
106 = 1.000.000
109 = 1.000.000.000
1020 = 100.000.000.000.000.000.000
Addicionalment, 10 elevat a una potència sencer negativa -n és igual a 1/10n o, equivalentment 0, (n-1 zeros) 1:
10-1 = 1/10 = 0,1
10-3 = 1/1000 = 0,001
10-9 = 1/1.000.000.000 = 0,000000001
Per tant un nombre com 156.234.000.000.000.000.000.000.000.000 pot ser escrit com a 1,56234 × 1029, i un nombre petit com a 0,0000000000234 pot ser escrit com 2,34 × 10-11.
Per exemple, la distància als confins observables del univers és ~4.6 × 1026m i la massa d'un protó és ~1,67 × 10-27 quilograms .
Dimensions (prefixes sistema mètric Internacional)
tera... x1012
giga... x109
megà... x106
Quilò... x103
hectò... x102
decà... x10
decí... x10−1
centí... x10−2
mil·lí... x10−3
micrò... x10−6
nanò... x10−9
picò... x10−12
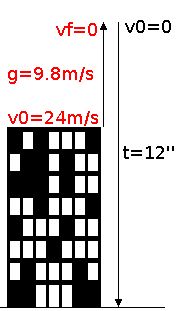 Primer podem esbrinar la distància des de l’alçada màxima fins el terra. Sabem que quan assoleix l’alçada màxima el cos està aturat, és a dir que la v0=0. L’acceleració és la de la gravetat a=9,8m/s2 i el temps és 12”. Apliquem la formula de inclou tots aquests ítems més el de la distància: d= Vo*t + 1/2 at2
Primer podem esbrinar la distància des de l’alçada màxima fins el terra. Sabem que quan assoleix l’alçada màxima el cos està aturat, és a dir que la v0=0. L’acceleració és la de la gravetat a=9,8m/s2 i el temps és 12”. Apliquem la formula de inclou tots aquests ítems més el de la distància: d= Vo*t + 1/2 at2