Moviment Rectilini Uniforme i Accelerat (MRUA)

El Moviment Rectilini Uniformement Accelerat (MRUA) és un tipus de moviment que té un cos sobre el qual s’aplica una força. La velocitat del cos serà variable i l’acceleració constant. Els ítems (expressats en les unitats del S.I) que poden participar d’aquest tipus de moviments són:
Velocitat inicial=Vo (m/s), velocitat final=Vf  (m/s), acceleració=a  (m/s2), temps=t(s), Distància=d (m)
Depenent de les dades que tinguem i les que ens demani el problema haurem d’aplicar una de les següents formules:    

Vf= Vo + at

Vf2= Vo2 + 2ad

d= Vo*t + 1/2 at2

(V0 + Vf) / 2 = d/t
 
La gravetat: un tipus de problemes de MRUA és el moviment dels cossos sota l’acceleració de la gravetat. La gravetat té una acceleració  aproximada de 9,8 m/s2 (de vegades d’accepta prendre 10 m/s2) i per simplificar encara més els problemes descartem altres forces que hi intervenen a la natura (vent, fricció,...)
Una dificultat recorrent és la confusió de la posició del cos i les forces que hi intervenen. Les magnituds cinemàtiques son vectorials i haurem d’establir l’inici i l’eix del moviment, el valor i signe de l’acceleració , el valor i el signe de la velocitat inicial i la posició inicial del cos. Després escrivim les equacions del moviment i a partir de les dades, aïllem les incògnites

Exercicis (amb solució)

1. Llencem verticalment i cap amunt un cos des de la vora de la terrassa d’un edifici amb una velocitat inicial de 24m/s. Triga 12” en caure des de l’alçada màxima que assoleix fins el terra. Quina alçada té l’edifici?

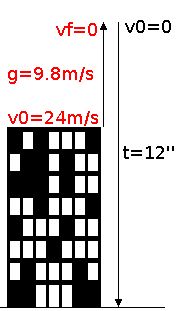Primer podem esbrinar la distància des de l’alçada màxima fins el terra. Sabem que quan assoleix l’alçada màxima el cos està aturat, és a dir que la v0=0. L’acceleració és la de la gravetat a=9,8m/s2 i el temps és 12”. Apliquem la formula de inclou tots aquests ítems més el de la distància: d= Vo*t + 1/2 at2
d= 0*t+ ½ 9.8*12;   d= 58,8m

Ara esbrinem la distància que hi ha des de la terrassa fins l’alçada màxima que assoleix el cos. Les dades que tenim són: v0=24m/s2, vf=0 i a=-9.8 perquè la força de la gravetat actúa en negatiu, frenant el cos en el seu ascens:
Amb l’equació de la velocitat Vf= Vo + at determinarem quant triga en aturar-se i assolir l’alçada màxima:
Vf= Vo + at ; o=24+-9.8*t; t=24/9.8; t=2,45”
El temps transcurregut es sustitueix a l’equació de la posició, Vf2= Vo2 + 2ad per obtenir la distància:
Vf2= Vo2 + 2ad;   0=242+2*-9,8*d;   0=576-19,6*d;   d=576/19,6;   d=29,8m
La diferència entre ambdues distàncies 58,8m-29.8=29m  és l’alçada de l’edifici.

2. Un cotxe que va a 120 km/h necessita 10 segons per aturar-s’hi. Quina desacceleració ha patit i quants metres necessita per parar?

Dades (S.I.): v0= 120 km/h = 33,33 m/s, vf= 0 m/s, t= 10s. Equacions:     vf = v0 + a.t     d = v0.t + ½ a.t ²


3. Un avió, quan toca la pista d’aterratge, frena amb una desacceleració de 20 m/s² i necessita 100 metres per aturar-se. Amb quina velocitat toca pista i quant triga en parar?

Dades (passades al S.I.):     a = - 20 m/s²    d = 100 m     vf = 0 m/s
De l’equació Vf2= Vo2 + 2ad traiem 0-v0 ² = 2ad; -v0 ² = 2(-20).(100); v0 ² = - 2(-20).(100); v0 ² = 4000;    
v0 ² = 4000;  v0: √4000;    v0=63,25 m/s
Per calcular el temps fem servir la formula  vf = v0 + a.t;   0 = v0 + at;    t = -v0/a   t = -63,25/- 20   t = 3,16 s